■記事リスト / ▼下のスレッド
/ ▲上のスレッド
□投稿者/ 避暑 一般人(1回)-(2024/08/06(Tue) 14:53:34)
 | 実数x,yに対して
2(x^2+1)(y^2+1)≧3(x+y)
が成り立つことの証明を教えて下さい。
|
|
|
▽[全レス3件(ResNo.1-3 表示)]
| ■52592 / ResNo.1) |
Re[1]: 不等式
|
□投稿者/ らすかる 一般人(12回)-(2024/08/06(Tue) 16:43:06)
 | (左辺)-(右辺)をxについて整理し平方完成する方針でいくと
2(x^2+1)(y^2+1)-3(x+y)
=2(y^2+1)x^2-3x+(2y^2-3y+2)
={x√{2(y^2+1)}-3/√{8(y^2+1)}}^2-9/(8(y^2+1))+(2y^2-3y+2)
={x√{2(y^2+1)}-3/√{8(y^2+1)}}^2+(16y^4-24y^3+32y^2-24y+7)/(8(y^2+1))
={x√{2(y^2+1)}-3/√{8(y^2+1)}}^2+{(4y^2-3y)^2+5(2y-1)^2+2(y-1)^2+y^2}/(8(y^2+1))
≧0
|
|
|
| ■52594 / ResNo.2) |
Re[2]: 不等式
|
□投稿者/ 避暑 一般人(2回)-(2024/08/08(Thu) 11:25:40)
 | 大変参考になりました。
有難うございました。
|
解決済み! |
|
| ■52596 / ResNo.3) |
Re[1]: 不等式
|
□投稿者/ muturajcp 一般人(4回)-(2024/08/10(Sat) 10:15:14)
 | へいほうかんせい
2(x^2+1)(y^2+1)-3(x+y)
=2(x^2+1)(y-3/{4(x^2+1)})^2+{(4x^2-3x)^2+23(x-12/23)^2+17/23}/{8(x^2+1)}>0
|
|
858×694 => 250×202
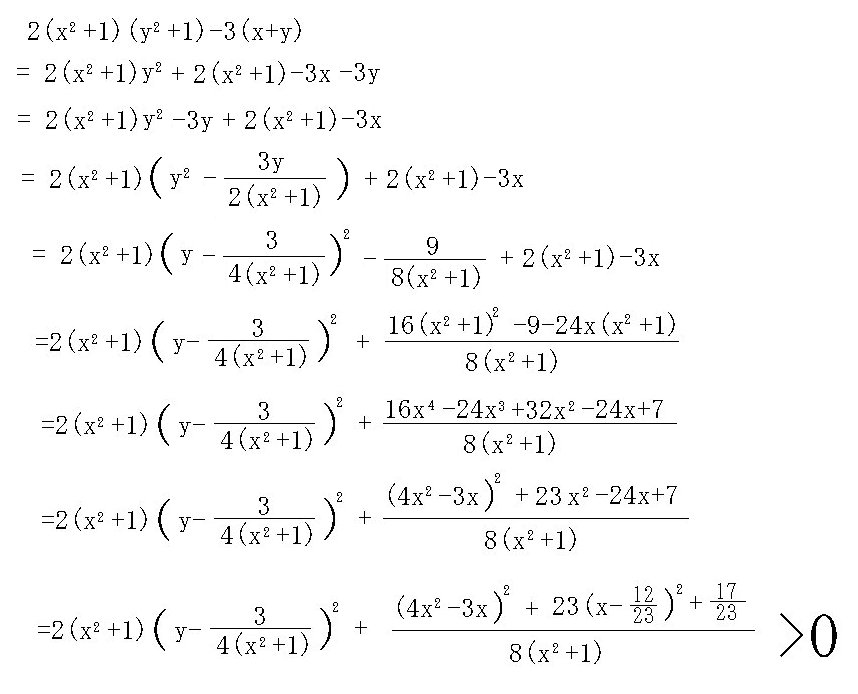
m2024080415.jpg/75KB
|
|
■記事リスト /
レス記事表示 →
[親記事-3]
|