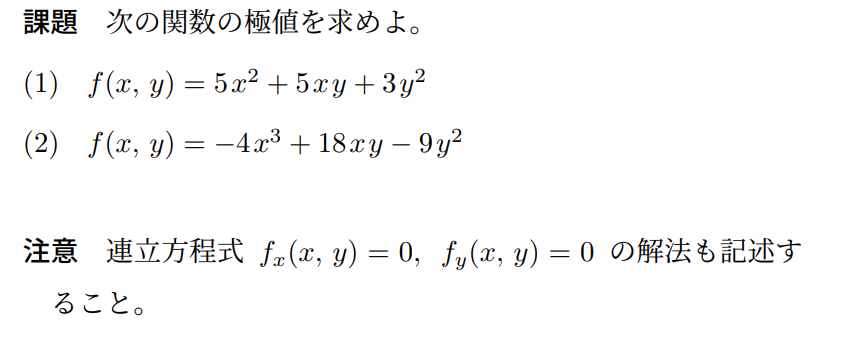| ■52144 / ResNo.1) |
Re[1]: 関数の極値
|
□投稿者/ muturajcp 一般人(5回)-(2023/03/31(Fri) 19:46:48)
 | (1)
f(x,y)
=5x^2+5xy+3y^2
=5(x+y/2)^2+7y^2/4≧0
(x,y)=(0,0) のときf(x,y)の最小値 0
(2)
f(x,y)
=-4x^3+18xy-9y^2
f_x=-12x^2+18y=0
-2x^2+3y=0
f_y=18x-18y=0
x-y=0
x=y
-2x^2+3x=0
x(3-2x)=0
x=0.or.x=3/2
(x,y)=(0,0).or.(x,y)=(3/2,3/2)
f_xx=-24x
f_xy=18
f_yy=-18
(f_xx)(f_yy)-(f_xy)^2=18*24x-18^2
(x,y)=(0,0)のとき
(f_xx)(f_yy)-(f_xy)^2=-18^2<0だから極値でない
(x,y)=(3/2,3/2)のとき
(f_xx)(f_yy)-(f_xy)^2=18*36-18^2>0
f_xx=-24*3/2=-36<0
極大値
f(3/2,3/2)
=-4(3/2)^3+18(3/2)^2-9(3/2)^2
=27/4
|
|