| ■50277 / ResNo.1) |
Re[1]: 正射影再び(笑)
|
□投稿者/ らすかる 一般人(10回)-(2020/04/11(Sat) 13:09:08)
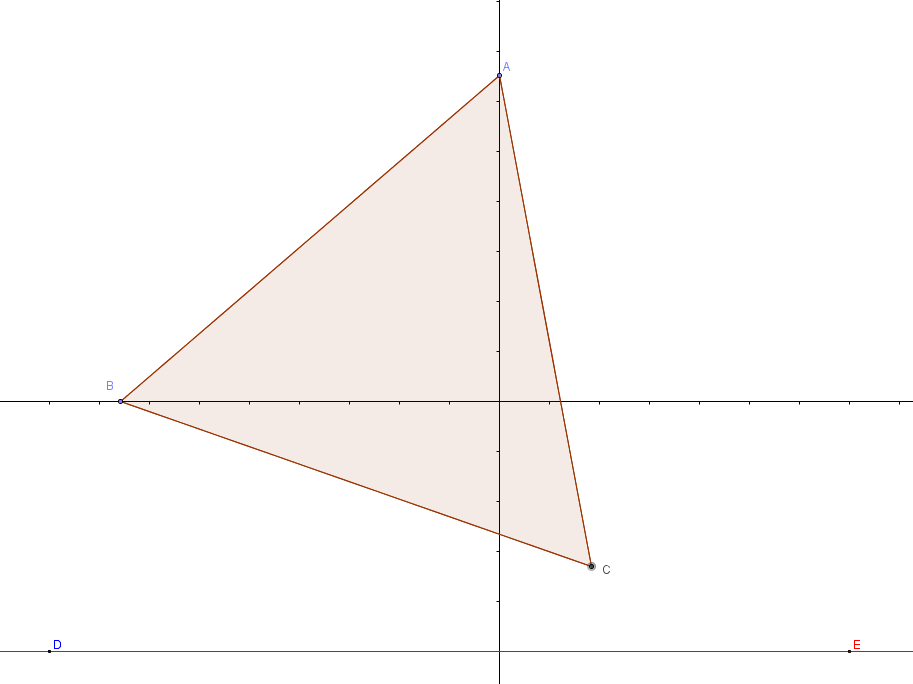
 | 図の正三角形が、正三角形の状態以外でBC=ACになることがあるか、
という質問なら、なることはありません。
なぜなら、回転軸に対して角度が大きい直線ほど
回転したときの縮小率が大きくなるからです。
よって正三角形以外の状態では常にAC<AB<BCとなります。
計算式で考えると、次のようになります。
Cを通りDEと平行な直線とA,BからDEにそれぞれ下した垂線の交点をP,Qとすると
AC=√(AP^2+CP^2)、BC=√(BQ^2+CQ^2)ですね。
このうち、CP,CQつまり水平成分は回転によって変わらず、
AP,BQつまり垂直成分が|cosθ|を掛けた長さになります。
すなわち
ACを回転すると√{(APcosθ)^2+CP^2}
BCを回転すると√{(BQcosθ)^2+CQ^2}
となるわけですね。
AC=BCなのでAP^2+CP^2=BQ^2+CQ^2ですが
AP>BQ,|cosθ|<1のとき
{(BQcosθ)^2+CQ^2}-{(APcosθ)^2+CP^2}
=(BQ^2-AP^2)(cosθ)^2+(CQ^2-CP^2)
=(BQ^2-AP^2)(cosθ)^2+(AP^2-BQ^2)
=(AP^2-BQ^2){1-(cosθ)^2}>0
よって
(BQcosθ)^2+CQ^2>(APcosθ)^2+CP^2
∴BC>AC
のようになります。
従って、正三角形を回転して二等辺三角形になるためには
2辺の回転軸に対する角度が同じ、つまり1辺が回転軸に垂直または平行
でなければいけないことがわかります。
逆に、1辺が回転軸に垂直または平行の場合に
回転して常に二等辺三角形になることは、
直感的に明らかですね。
|
|