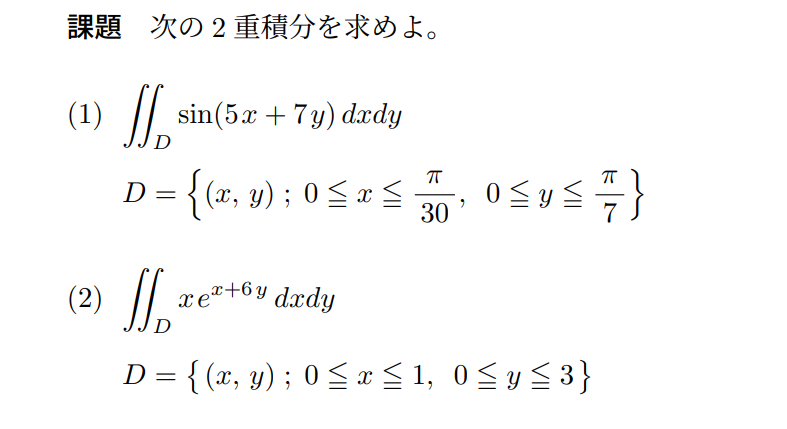■記事リスト / ▼下のスレッド
/ ▲上のスレッド
□投稿者/ アルティメットテンパイ 一般人(14回)-(2023/01/26(Thu) 17:42:02)
 | 計算の過程もお願いします
二重積分の問題です、よろしくお願いします。
|
|
804×523 => 250×162

suugaku11.png/76KB
|
|
▽[全レス4件(ResNo.1-4 表示)]
| ■52100 / ResNo.1) |
Re[1]: 二重積分
|
□投稿者/ 花火 一般人(5回)-(2023/01/26(Thu) 17:48:39)
 | 大学の課題でしょうか?
しっかり考えましょう。
私はこれ以上あなたの投稿への回答は差し控えます。
数学でなく単位の取り方を勉強している大学生に知恵を貸すつもりはありません。
|
|
|
| ■52101 / ResNo.2) |
Re[2]: 二重積分
|
□投稿者/ アルティメットテンパイ 一般人(19回)-(2023/01/26(Thu) 17:56:29)
 | 後期は大学にほとんど出席できなかったため、残り二週間でこれらの課題を解くことができないと感じたためこのサイトを利用させていただきました。
申し訳ございません。
|
|
|
| ■52102 / ResNo.3) |
Re[3]: 二重積分
|
□投稿者/ 花火 一般人(6回)-(2023/01/26(Thu) 18:12:11)
 | どのような理由であれ、最終的には自己責任です。他力本願にもほどがあります。
とりあえず教科書の例題を読み、1問でも多く解いて提出しましょう。
全部に目をとおしていませんが、どれも多変数関数の基本的な内容の問題だとおもいます。多少計算が大変そうなものもありますが、いずれも類題が問題集などに載っていると思われます。
|
|
|
| ■52103 / ResNo.4) |
Re[4]: 二重積分
|
□投稿者/ アルティメットテンパイ 一般人(20回)-(2023/01/26(Thu) 18:38:01)
 | そうですね、一つずつ解いていこうと思います。
残り15個あるので頑張ろうと思います。
参考書等を参照してもわからない問題は質問させていただこうと思います。
返信ありがとうございました。
|
|
|
■記事リスト /
レス記事表示 →
[親記事-4]
|