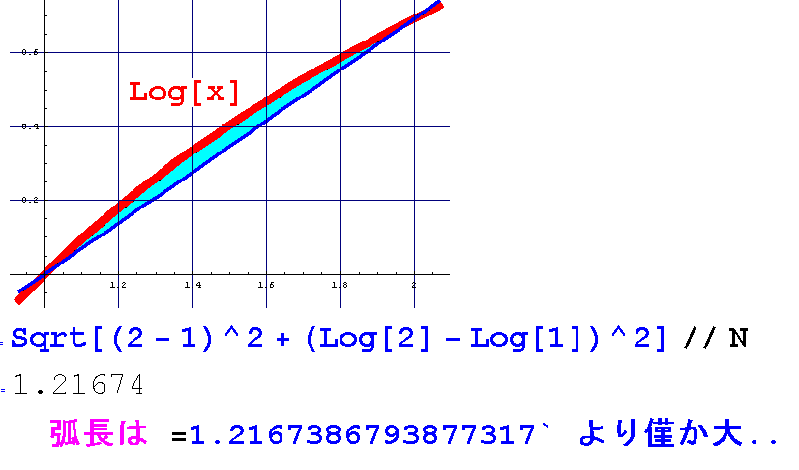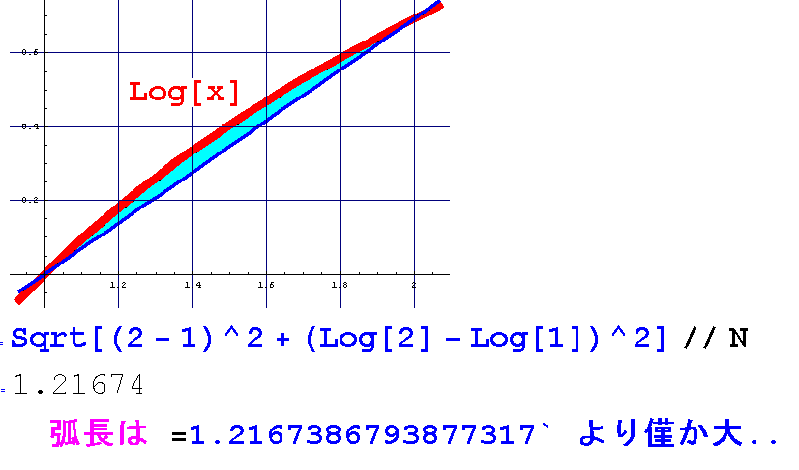| Arc‚³‚ٌ‚²ژw“E‚ ‚è‚ھ‚ئ‚¤‚²‚´‚¢‚ـ‚·پB
sumika‚³‚ٌ‚²‚ك‚ٌ‚ب‚³‚¢پBŒvژZٹشˆل‚¢‚ً‚µ‚ؤ‚¢‚ـ‚µ‚½‚ج‚إ’ùگ³‚µ‚ـ‚·پB
L = پç[پم2-1,پم5-2]{(1+t^2)/(1-t^2)}*{(-1/2)(1+t^2)/(t^2)}dt
‚ـ‚إ‚حگ³‚µ‚¢‚ئژv‚¢‚ـ‚·پBˆب‰؛’ùگ³‚µ‚ـ‚·پB
L = (-1/2)پç[پم2-1,پم5-2]{((1+t^2)^2)/((1-t^2)(t^2))}dt
‚ئ‚ب‚è‚ـ‚·پB
1/((1-t^2)(t^2)) = 1/(1-t^2)+1/(t^2), 1/(1-t^2) = (1/2){1/(1-t)+1/(1+t)}
‚إ‚·‚ج‚إپA
((1+t^2)^2)/((1-t^2)(t^2)) = (1+2t^2+t^4)*{1/(1-t^2)+1/(t^2)}
= (4-2(1-t^2)-(1-t^4))/(1-t^2)+(1/t^2+2+t^2)
= (4/(1-t^2)-2-(1+t^2))+(1/t^2+2+t^2)
= 4/(1-t^2)-1+1/t^2
= 2/(1-t)+2/(1+t)-1+1/t^2
‚و‚ء‚ؤپA
L = (-1/2)پç[پم2-1,پم5-2]{2/(1-t)+2/(1+t)-1+1/t^2}dt
= (-1/2)[-2*log(1-t)+2*log(1+t)-t-1/t]_[پم2-1,پم5-2]
= [log((1-t)/(1+t))+t/2+1/(2t)]_[پم2-1,پم5-2]
F(t) = log((1-t)/(1+t))+t/2+1/(2t)‚ئ‚¨‚‚ئپAL = F(پم5-2)-F(پم2-1)‚إ‚·پB
F(پم5-2) = log((1-(پم5-2))/(1+(پم5-2)))+(پم5-2)/2+1/(2*(پم5-2))
= log((3-پم5)/(پم5-1))+(پم5-2)/2+(پم5+2)/(2*(5-4))
= log((3-پم5)(پم5+1)/(5-1))+(پم5-2)/2+(پم5+2)/2
= log((2پم5-2)/4)+پم5
= log((پم5-1)/2)+پم5
F(پم2-1) = log((1-(پم2-1))/(1+(پم2-1)))+(پم2-1)/2+1/(2*(پم2-1))
= log((2-پم2)/(پم2))+(پم2-1)/2+(پم2+1)/2
= log(پم2-1)+پم2
ˆبڈم‚©‚ç
L = {log((پم5-1)/2)+پم5}-{log(پم2-1)+پم2} = 1.2220¥¥¥¥¥
‚ئ‚ب‚è‚ـ‚·پB
|