 | こんばんは。また悩んでいる問題があったので、質問させていただきます。
【1】線積分
C:|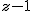 |= 2 のとき、次の線積分を求めよ。 |= 2 のとき、次の線積分を求めよ。
}%5cright)dx}
)
まず、) =0を計算して、z=0、2、-2が求まりました。ここでf(z)は3つの極z=±2、z=0をもち、Cの内部にあるのはZ=2、Z=0が出ましたが、Z=0の計算でどうしても分母が0になってしまい計算できません・・・ =0を計算して、z=0、2、-2が求まりました。ここでf(z)は3つの極z=±2、z=0をもち、Cの内部にあるのはZ=2、Z=0が出ましたが、Z=0の計算でどうしても分母が0になってしまい計算できません・・・
もしかしてZ=0は極ではないのですか?
【2】定積分
次の定積分を求めよ。
}{x^2+c^2}%5cright)dx}
)
積分範囲:-∞ から ∞
答えはe^(-bc)πなんですが、どうやって求めるのでしょうか?
【3】確率統計
確率変数Xが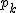 =(1-λ)λ^k、k=0,1,2,・・・、0<λ<1を確率関数とするとき =(1-λ)λ^k、k=0,1,2,・・・、0<λ<1を確率関数とするとき
(1)Xが偶数になる確率を求めよ。
(2)Xの母平均ν=E(X)を求めよ。
これも分かりません。
よろしくお願いします。
|