| ■25722 / inTopicNo.4) |
Re[1]: 複素平面上の問題(複素数)
|
□投稿者/ miyup 大御所(1237回)-(2007/06/17(Sun) 17:11:12)
 | ■No25716に返信(CERMETさんの記事)
> 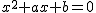 の解をα,βとする。 の解をα,βとする。
> 複素平面において3点1,α,βが原点を中心とする円に内接する正三角形の頂点になるような、定数a,bを求めよ。
>
> 自分で考えは、α=A+Bi,β=C+Diとおき、正三角形の座標を(1,0),(A,B),(C,D)とおいてA,B,C,Dをだす、というものなのですが、肝心のA,B,C,Dの求め方が分かりません。
むしろ先に図を描いた方がいいと思います。
そうすればすぐに、α,βが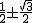 になることがわかります。 になることがわかります。
|
|