| ■42089 / inTopicNo.2) |
Re[1]: 接線
|
□投稿者/ tokoro 一般人(32回)-(2010/07/07(Wed) 18:29:54)
 | 2010/07/07(Wed) 18:31:14 編集(投稿者)
2つの放物線を、
%20=%20x^2%20%5c%20%5c%20%5c%20,%20%5c%20%5c%20%5c%20f_{2}(x)%20=%20-%20x^2%20+%20a%20x%20-%202)
とします。
この1次導関数は、
%20=%202x%20%5c%20%5c%20%5c%20,%20%5c%20%5c%20%5c%20f_{2}^{%5cprime}(x)%20=%20-%202x%20+%20a)
です。
まず、2つの放物線が共有点を持つためには、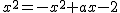 から、 から、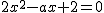
これが実数解を持つのは判別式から、(a%20-%204)%20%5cgeq%200) となります。 となります。
しかし、図を描けば明らかなように、一点で2つの放物線が接する場合でないと、2つの放物線で共通の接線にはなりません。
したがって、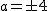 が解です。 が解です。
以下、検算
(1) 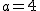 の場合 の場合
^2%20=%200) より、 より、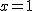 が共有点の が共有点の 座標になり、 座標になり、%20=%20(1,%20%5c%201)) が共有点。 が共有点。
このとき、2つの放物線の接線の傾きは、
%20=%202%20%5c%20%5c%20%5c%20,%20%5c%20%5c%20%5c%20f_{2}^{%5cprime}(1)%20=%20-%202%20+%204%20=%202)
で共通であり、接線は、) から、 から、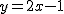
(2) 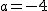 の場合 の場合
^2%20=%200) より、 より、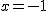 が共有点の が共有点の 座標になり、 座標になり、%20=%20(-%201,%20%5c%201)) が共有点。 が共有点。
このとき、
2つの放物線の接線の傾きは、
%20=%20-%202%20%5c%20%5c%20%5c%20,%20%5c%20%5c%20%5c%20f_{2}^{%5cprime}(-%201)%20=%202%20-%204%20=%20-%202)
で共通であり、接線は、) から、 から、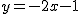
|
|