 | \section{フェルマー数}
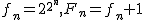 とおき, 数列を とおき, 数列を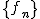 と と 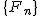 を考える. を考える.
ただし 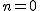 から始める.(部分的に 月号の内容とダブル部分がある. ) から始める.(部分的に 月号の内容とダブル部分がある. )
定義により,
^2=2^{2^{n+1}}=f_{n+1}.
)
ゆえに
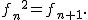
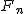 を\textbf{フェルマー数}という. を\textbf{フェルマー数}という.
% 表
\begin{table}[ht]
\caption{フェルマーの数}%{}内に表題を書く
\begin{center}
\begin{tabular}{ccc}
 & & 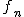 & & 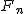 \\ \\
\hline
0 & 2 & 3 \\
1 & 4 & 5 \\
2 & 16 & 17 \\
3 & 256 & 257 \\
4 & 65536 & 65537 \\
\end{tabular}
\end{center}
\end{table}
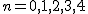 のときのフェルマー数はみな素数である. のときのフェルマー数はみな素数である.
素数のとき \textbf{フェルマー素数}という.
フェルマーは 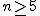 のときも のときも 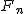 は素数であると思ったが は素数であると思ったが
それは正しくなかった.
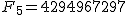 はオイラーにより素因数分解された: はオイラーにより素因数分解された:
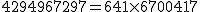
実は皮肉なことに 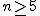 のとき素数になるフェルマー数(すなわち,フェルマー素数 )は のとき素数になるフェルマー数(すなわち,フェルマー素数 )は
未だに1つも発見されていない.
\subsection{フェルマー数の積}
フェルマー数の積を, 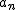 すなわち すなわち 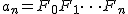 とおく. とおく.
すると,定義から
 a_{n+1}=F_0F_1 \cdots F_{n+1}=a_nF_{n+1} a_{n+1}=F_0F_1 \cdots F_{n+1}=a_nF_{n+1} 
なので 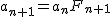 . .
\subsection{補題}
\begin{lemma}
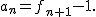
\end{lemma}
を帰納法で示す.
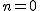 なら成立.実際, なら成立.実際, 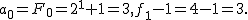
\
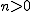 のとき, のとき, 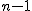 の場合を仮定すると, の場合を仮定すると,(f_{n}+1)) によって によって
(f_{n}+1)=(f_{n})^2-1=f_{n+1}-1.
)
\newpage
\subsection{=-1) の証明} の証明}
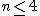 について について 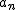 のオイラー関数の値を のオイラー関数の値を 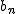 とおけば とおけば
これらの 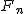 はフェルマー素数なので はフェルマー素数なので =f_n) により により
%20) なので なので 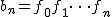 となる. となる.
このとき
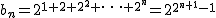
なので
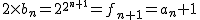
を満たす.
よって,
=a_{n}-2b_n=-1.
)
% 表
\begin{table}[ht]
\caption{フェルマー数の積}%{}内に表題を書く
\begin{center}
\begin{tabular}{c|ccc}
 & & 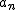 & 素因数分解 & & 素因数分解 & 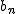 \\ \\
\hline
1 & 3 & [3] & 2 \\
2& 15 & [3,5] & 8 \\
3& 255 & [3,5,17] & 128 \\
4& 65535 & [3,5,17,257] & 32768 \\
\end{tabular}
\end{center}
\end{table}
\subsection{未解決の問題}
\textbf{研究課題}
=-1) を満たす を満たす  は上の表に載っているものだけか ? は上の表に載っているものだけか ?
\
これは難しい問題であろう. しかし分かることが少しある.少し示そう.
\begin{equation} \label{mikai}
a-2\varphi(a)=-1
\end{equation}
を満たすとき,  の素因子の指数は1である. の素因子の指数は1である.
実際,  の素因子 の素因子 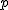 の指数 の指数  があり があり 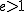 とすると とすると
) も も 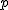 の倍数なので の倍数なので ) も も
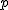 の倍数になり式 (\ref{mikai}) に矛盾する. の倍数になり式 (\ref{mikai}) に矛盾する.
\
さて -1) なので なので  は奇数である. は奇数である.
\
1.  は3を素因数に持つと仮定する. は3を素因数に持つと仮定する.
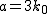 と書くとき, と書くとき, 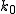 は3で割れないから式 (\ref{mikai})に注意して は3で割れないから式 (\ref{mikai})に注意して
=2%5cvarphi(3k_0)=4%5cvarphi(k_0)=a+1=3k_0+1.
)
ゆえに
\begin{equation}
3k_0+1=4\varphi(k_0).
\end{equation}
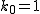 のとき, のとき, -1=4-1=3) なので なので 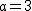 は解. は解.
\
2.
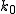 が 5 を素因数に持つと仮定する. が 5 を素因数に持つと仮定する. 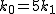 とおくと とおくと
=4%20%5cvarphi(5k_1)=4^2%5cvarphi(k_1),
)
と 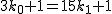 により により
.
)
\
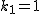 のとき, のとき, -1=2%20%5ctimes%202%20%5ctimes%204-1=15) なので なので 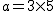 は解. は解.
の記法によれば 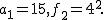 ここで ここで 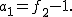
\
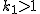 のとき, のとき, 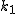 の最小素因数を の最小素因数を 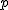 とすると とすると 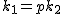 と書けて と書けて 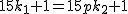 , さらに , さらに
=4^2%5cvarphi(pk_2)=4^2%20%5ctimes%20(p-1)%20%5cvarphi(k_2)%20%5cleq%204^2%20%5ctimes%20(p-1)k_2
)
によって
k_2.
)
これを変形して
%20-15p)k_2=(p-16)k_2.
)
3.
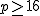 かつ素数なので かつ素数なので 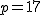 とおいてみる.すると とおいてみる.すると
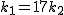 , ,
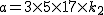 によって, によって,
=2%5cvarphi(3%20%5ctimes%205%20%5ctimes%2017%5ctimes%20k_2)=2%20%5ctimes%202%20%5ctimes%204%20%5ctimes%2016%5ctimes%20%5cvarphi(k_2).
)
よって
-1.
)
の記法によれば 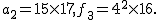 これより これより
-1
)
\
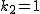 のとき のとき 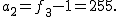 これは これは =f_3=a_2+1) により により
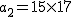 が解になる. が解になる.
\
4. 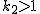 のとき のとき
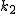 の最小素因数を の最小素因数を 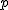 とすると とすると 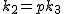 と書けて と書けて
-1=f_3%20(p-1)%5cvarphi(k_3)-1<f_3%20(p-1)k_3-1.
)
\begin{equation}
1< - a_2 p k_3+f_3 (p-1)k_3=(- a_2 p +f_3 (p-1) ) k_3=(p-f_3)k_3
\end{equation}
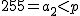 であり 257は素数なので であり 257は素数なので 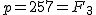 とおく. とおく.
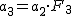 なので なので
^2%20%5cvarphi(k_3)-1=f_4%20%5cvarphi(k_3)-1.
)
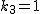 のとき のとき  が解. が解.
\
5. 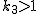 のとき のとき
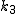 の最小素因数を の最小素因数を 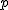 とすると とすると 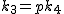 と書けて と書けて
-1=f_4%20(p-1)%5cvarphi(k_4)-1<f_4%20(p-1)k_4-1.
)
\begin{equation}
1< - a_3 p k_4+f_4 (p-1)k_4=(- a_3 p +f_4 (p-1) ) k_4=(p-f_4)k_4.
\end{equation}
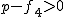 により により 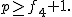 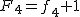 は素数なので は素数なので 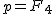 とおけば とおけば
%5cvarphi(k_4)-1.
)
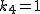 とおけば とおけば 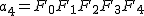 が解になる. が解になる.
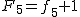 は素数では無い. したがってここで終わる. は素数では無い. したがってここで終わる.
\
|