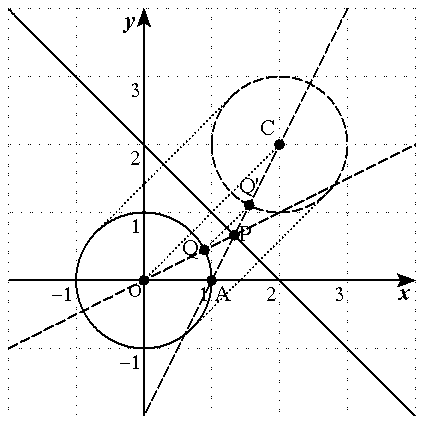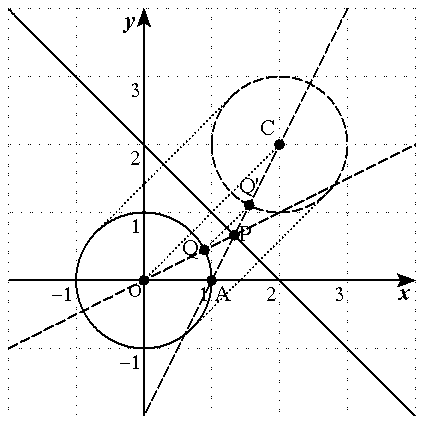| 2009/08/02(Sun) 23:30:07 編集(投稿者)
円x^2+y^2=1を直線x+y=2に関して対称移動した円(x−2)^2+(y−2)^2=1を考えると、
4点A, P, Q'(円(x−2)^2+(y−2)^2=1の周上の点), C(円(x−2)^2+(y−2)^2=1の中心)が
この順で同一直線上に存在するとき、AP+PQ'は最小になります。
さらに、
3点P, Q(円x^2+y^2=1の周上の点), O(円x^2+y^2=1の中心)が
この順で同一直線上に存在するとき、AP+PQも最小になり、AP+PQ'の最小値と同じになります。
AP+PQ(AP+PQ')の最小値は、図を見ると割りと簡単に計算できます。(AC−Q'C)
点Pは(t,2−t)とおいて、直線ACの式に代入することで求めることができます。
点QはOQを斜辺とする直角三角形を考えて三角比より求めた方が楽かと思います。
> Xさん
Xさんの後に勝手に書き込んだ形になり、申し訳ございません。
|