 | Oを原点にとる。
⊿BCDをxy面に平行にとると
OB=OC=OD(=4)から
⊿BCDの外心Eはz軸上にとれる。
⊿BCDの外接円の半径rは
r=√{16-h^2}
BDをx軸と平行にとり、
⊿BCDを含む面Sの原点からの距離をhとすれば
E:(0,0,h)
S:z=h
BCDを固定すると、体積が最大となるAの位置は
(0,0、-1)
BDの中点Mはyz面上だから
B(rX,0,h) D(-rX,0,h)
とおいてもいい。(BD=2rX)
⊿BCDが最大となるのは、Cがyz面上のとき(MCとBDが直角のとき)
だから(⊿BCDは2等辺三角形)
C(0,r,h)
だから、
M:(0,-rY,h)
とおくと
MC=CE+EM=r(1+Y)
Y=√{1-X^2}
⊿BCDの面積をS1とすれば
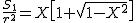
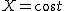
とすれば(t=∠EBC=∠ECB)
!
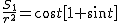
(}%5csin%20%20%20t{%5crm%20%20-%20}%5cfrac{{%5crm%201}}{{%5crm%202}}{%5crm%20)}%20%5c%5c%20
%20%5cend{array}
)
から
t=π/6、X=√3/2
で最大(⊿BCDが正三角形のとき)
S1=3√3/4r^2
四面体ABCDの体積をVとすると
V=S1×(1+h)/3 :r=√{16-h^2}
=√3/4(16-h^2)(1+h)
V'=(16-h^2)(1+h)
dV'/dt=-(h-2)(3h+8)
h=2で最大
V=9√3
|