 | ken����C������D
> �܂��A�A�X�e���C�h�̖��ŁA�Ȃ�0���Ɓ���/2�Ȃ̂ł����H
> �l��0���Ɓ��ōl���Ă����̂ł����c
�A�X�e���C�h�̂����C���ی��̕����݂̂��l���Ă��邩��ł��D
�A�X�e���C�h�́C �C �C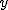 ���Ɋւ��Đ��Ώ̂Ȃ̂ŁC���ی��̕����� ���Ɋւ��Đ��Ώ̂Ȃ̂ŁC���ی��̕����� ���̎���ɉ�]���ē���ꂽ�Ȗʂ̋Ȗʐς� ���̎���ɉ�]���ē���ꂽ�Ȗʂ̋Ȗʐς�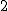 �{�����OK�ł��D �{�����OK�ł��D
�������Cken����̍l����ꂽ�C �ł����܂��܂���D���̏ꍇ�́C���C��ی��̕������l���Ă��邱�ƂɂȂ�܂��D�������C�ϕ����鎞�ɏ�[/���[�𒍈ӂ���K�v������܂��˂��`�D �ł����܂��܂���D���̏ꍇ�́C���C��ی��̕������l���Ă��邱�ƂɂȂ�܂��D�������C�ϕ����鎞�ɏ�[/���[�𒍈ӂ���K�v������܂��˂��`�D
=(a,0)) �C �C
=(-a,0))
�ƑΉ����Ă��܂��̂ŁC�ϕ����v�Z����Ƃ��́C

�ƂȂ�܂��D
> ���ɁA�~�̉�]�̖̂��ł����c
> ����͔}��ϐ��\���Gx=rcos��,y-b=rsin�Ƃ�p���ĉ������Ƃ͏o���Ȃ��̂ł����H
�o���܂���D
�������C������ϕ��͈͂ɒ��ӂ���K�v������܂��D
�l�̐����́C
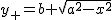
�̕����́C�p�����[�^�\������ƁC

)
�܂��C

�̕����́C�p�����[�^�\������ƁC

)
�ł��D�]���āC
'^{2}+1}dx%20+%20%5cdisplaystyle%5cint_{-a}^{a}y_{-}%5csqrt{(y_{-})'^{2}+1}dx%20%5c%5c
)
�����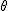 �Ɋւ���ϕ��ɕϊ����邾���ł��D����ƁC �Ɋւ���ϕ��ɕϊ����邾���ł��D����ƁC

�ƂȂ�܂��D �̒����ǂ��Ȃ邩�́Cken����̕��Ōv�Z���Ă݂Ă��������D �̒����ǂ��Ȃ邩�́Cken����̕��Ōv�Z���Ă݂Ă��������D
>
> �O�p���̗̈�̖��͂ƂĂ������ł��܂����I�I���肪�Ƃ��������܂��I�I�I
> �c�����A�l�̍l�����Łc�Ƃƃӂ͈͍̔͂����Ă���ł��傤���H�H
----ken����̍l����-------------------------------------------------
��(x/6)=rsin��cos��, ��(y/3)=rsin��sin��,��(z/2)=rcos��
��={(r,�ƁC��)|0��r��1,0���Ɓ���/2,0���Ӂ���/2}�@�Ƃ����āA
�v�Z����Ƃ������@�ɂȂ����̂ł����A���͈̔͂ɏ����n�k������܂���c
---------------------------------------------------------------------
�� �͈̔͂ł����C����ł����Ă܂��悧�`�D �͈̔͂ł����C����ł����Ă܂��悧�`�D
�������C���̂悤�ɋ��ʋɍ��W�ɕϊ������ꍇ�́C

�ƂȂ�̂ŁC%5cto(r,%5ctheta,%5cphi)) �ƕϊ������Ƃ��̃��R�r�A���̌v�Z������̂����ɖʓ|�L�����ł��D �ƕϊ������Ƃ��̃��R�r�A���̌v�Z������̂����ɖʓ|�L�����ł��D
|