 | 2006/08/06(Sun) 00:49:49 編集(投稿者)
問題を解いていて分からないところがありましたので質問させてください。
t<3,t≠1であるtに対応して、x^2/(3-t) + y^2/(1-t) = 1 によってあらわされるxy平面上の曲線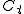 を考える。a≠0,b≠0として平面上の定点A(a,b)をとる。 を考える。a≠0,b≠0として平面上の定点A(a,b)をとる。
(1)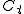 が点Aを通るようなtは2つあることを証明せよ。 が点Aを通るようなtは2つあることを証明せよ。
(2)上の二つのtを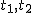 とするとき、曲線 とするとき、曲線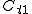 , ,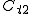 のうち一つは楕円でもう一つは双曲線であることを証明せよ。 のうち一つは楕円でもう一つは双曲線であることを証明せよ。
(3)(2)の曲線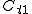 , ,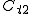 の点Aにおける2つの接線は直行することを証明せよ。 の点Aにおける2つの接線は直行することを証明せよ。
という問題で、(1)から躓いております。(a,b)を代入してtの二次関数にして、
t<3,t≠1で異なる二つの実数解を持つことを示せばよいような気がするのですが、
どうも上手くできそうにありません。
どなたよろしくお願い致します。
|