 | 2010/07/14(Wed) 08:40:06 編集(投稿者)
2010/07/14(Wed) 08:34:32 編集(投稿者)
こういう問題は、いくつか比較的簡単に求められるものを、実際に求めてみることをお勧めします。
オイラーの公式を使った方法2の方が簡単です。
<方法1>
まず、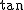 の加法公式は、次の通りです。 の加法公式は、次の通りです。
%20=%20%5cfrac{%5ctan%20%20%20%5calpha%20+%20%5ctan%20%20%20%5cbeta}{1%20-%20%5ctan%20%20%20%5calpha%20%5ctan%20%20%20%5cbeta})
よって、2倍角の公式は、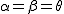 として、 として、
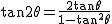
3倍角の場合、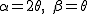 として、 として、
%20=%20%5cfrac{%5ctan%20%20%202%20%5ctheta%20+%20%5ctan%20%20%20%5ctheta}{1%20-%20%5ctan%20%20%202%20%5ctheta%20%5ccdot%20%5ctan%20%20%20%5ctheta})
となりますが、2倍角の結果を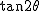 のところに代入して( のところに代入して(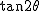 の分母の の分母の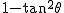 に注意)、 に注意)、
}{(1%20-%20%5ctan%20%20^2%20%5ctheta)%20-%202%20%5ctan%20%20%20%5ctheta%20%5ccdot%20%5ctan%20%20%20%5ctheta}
=
%5cfrac{3%20%5ctan%20%20%20%5ctheta%20-%20%5ctan%20%20^3%20%5ctheta}{1%20-%203%20%5ctan%20%20^2%20%5ctheta})
<方法2>
オイラーの公式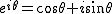 より、 より、
指数関数の性質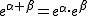 を使って考えます。 を使って考えます。
2倍角の場合、
}%20=%20e^{i%20%5ctheta}%20%5ccdot%20e^{i%20%5ctheta}%20=%20(%5ccos%20%20%20%5ctheta%20+%20i%20%5csin%20%20%20%5ctheta)^2
=
(%5ccos%20%20^2%20%5ctheta%20-%20%5csin%20%20^2%20%5ctheta)%20+%20i%20(2%20%5csin%20%20%20%5ctheta%20%5ccos%20%20%20%5ctheta))
となりますが、実数部分は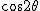 、虚数部分は 、虚数部分は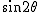 の加法公式を意味するので、 の加法公式を意味するので、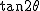 は、分子に虚数部分、分母に実数部分をあてると、 は、分子に虚数部分、分母に実数部分をあてると、
}{(%5ccos%20%20^2%20%5ctheta%20-%20%5csin%20%20^2%20%5ctheta)}
=
%5cfrac{2%20%5ctan%20%20%20%5ctheta}{1%20-%20%5ctan%20%20^2%20%5ctheta})
となって、方法1の結果と同じものが得られます。
3倍角も同様に、
}%20=%20(%5ccos%20%20%20%5ctheta%20+%20i%20%5csin%20%20%20%5ctheta)^3
=
(%5ccos%20%20^3%20%5ctheta%20-%203%20%5ccos%20%20%20%5ctheta%20%5csin%20%20^2%20%5ctheta)%20+%20i%20(3%20%5ccos%20%20^2%20%5ctheta%20%5csin%20%20%20%5ctheta%20-%20%5csin%20%20^3%20%5ctheta))
となるので、先と同様に、分子に虚数部分、分母に実数部分をあてると、
}{(%5ccos%20%20^3%20%5ctheta%20-%203%20%5ccos%20%20%20%5ctheta%20%5csin%20%20^2%20%5ctheta)}
=
%5cfrac{(3%20%5ctan%20%20%20%5ctheta%20-%20%5ctan%20%20^3%20%5ctheta)}{(1%20-%203%20%5ctan%20%20^2%20%5ctheta)})
となって、方法1の結果と同じものが得られます。
さて、問題は、一般のm倍角の加法公式と2項係数の関係を求めることです。
2項係数とは、
^n%20=%20%5csum_{k%20=%200}^{n}%20{}_{n}%20C_{k}%20a^{(n%20-%20k)}%20b^{k}
=
a^{n}%20+%20n%20a^{(n%20-%201)}%20b%20+%20%5cfrac{n%20(n%20-%201)}{2}%20a^{(n%20-%202)}%20b^{2}%20+%20%5ccdots%20+%20n%20a%20b^{(n%20-%201)}%20+%20b^{n})
の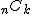 のことです。 のことです。
以上で求めた3倍角までの公式で、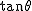 のベキの前にかかっている係数が、この2項係数になるわけです。 のベキの前にかかっている係数が、この2項係数になるわけです。
これをもっとはっきりと示すには、オイラーの公式を使う方法を少し変形して、次のようにします。
)
ここで、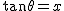 とおくと、5倍角まで、 とおくと、5倍角まで、
^2%20=%20(1%20-%20x^2)%20+%20i%20(2%20x))
^3%20=%20(1%20-%203%20x^2)%20+%20i%20(3%20x%20-%20x^3))
^4%20=%20(1%20-%206%20x^2%20+%20x^4)%20+%20i%20(4%20x%20-%204%20x^3))
^5%20=%20(1%20-%2010%20x^2%20+%205%20x^4)%20+%20i%20(5%20x%20-%2010%20x^3%20+%20x^5))
となります。
よって、一般のm倍角の加法公式は、
^{m}%20=%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%201^{(m%20-%20k)}%20(i%20x)^{k}
=
%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i%20x)^{k}
=
Re%20%5c{%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i%20x)^{k}%20%5c}%20+%20i%20%5ccdot%20Im%20%5c{%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i%20x)^{k}%20%5c})
より、

=
%5cfrac{%5csum%20a_{j}%20(%5ctan%20%20%20%5ctheta)^{j}}{%5csum%20b_{k}%20(%5ctan%20%20%20%5ctheta)^{k}}
=
%5cfrac{Re%20%5c{%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i%20x)^{k}%20%5c}}{Im%20%5c{%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i%20x)^{k}%20%5c}}
=
%5cfrac{Re%20%5c{%20%5csum_{j%20=%200}^{m}%20{}_{m}%20C_{j}%20(i)^{j}%20(%5ctan%20%20%20%5ctheta)^{j}%20%5c}}{Im%20%5c{%20%5csum_{k%20=%200}^{m}%20{}_{m}%20C_{k}%20(i)^{k}%20(%5ctan%20%20%20%5ctheta)^{k}%20%5c}}
)
と表すことができます。
ここで、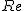 は実数部部を、 は実数部部を、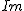 は虚数部分をとることを意味します。 は虚数部分をとることを意味します。
つまり、係数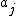 は実数部分の2項係数、係数 は実数部分の2項係数、係数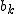 は虚数部分の2項係数になります。 は虚数部分の2項係数になります。
(正確には、さらに虚数単位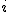 が偶数回・奇数回かけられての正負の符号を考慮したもの。上の式の関係の通り) が偶数回・奇数回かけられての正負の符号を考慮したもの。上の式の関係の通り)
例えば2倍角の場合、
^2%20=%20%5csum_{k%20=%200}^{2}%20{}_{2}%20C_{k}%20(i%20x)^{k}
=
{}_{2}%20C_{0}%20(i%20x)^{0}%20+%20{}_{2}%20C_{1}%20(i%20x)^{1}%20+%20{}_{2}%20C_{2}%20(i%20x)^{2}
=
1%20+%202%20(i%20x)%20+%20(-%20x^2))
より、
^2%20%5c}%20=%20(1%20-%20x^2),%20%5c%20Im%20%5c{%20(1%20+%20i%20x)^2%20%5c}%20=%202%20x,%20%5c%20%5ctan%20%20%20(2%20%5ctheta)%20=%20%5cfrac{2%20x}{1%20-%20x^2}
=
%5cfrac{2%20%5ctan%20%20%20%5ctheta}{1%20-%20(%5ctan%20%20%20%5ctheta)^2})
となるわけです。
|