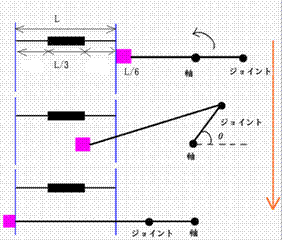
| r≪a であれば黒い四角は中央でよいですが、そうでなければ
中央より右になりますね。
極端な例、たとえばr=1, a=1.01 という例を考えてみると、
1.01-1=0.01, √(1.01^2-1^2)=0.14, 1.01+1=2.01 ですから、
θ=0°〜90°の範囲では紫色の物体は0.13しか動きませんが、
θ=90°〜180度の範囲で1.87も動きます。
この例では、黒い四角の位置は右端に近いですね。
実際にどこに置けばよいかは
f(θ)=√{a^2-(rsinθ)^2}-rcosθ-(a-r) として
f(180°-θ)-f(θ)=L/2 を解けば出せます。
f(180°-θ)-f(θ)=2rcosθ であり
2r=(7/6)L ですから
2rcosθ=(7/6)Lcosθ=L/2
∴cosθ=3/7
黒い四角の右端の位置は
f(θ)=√{a^2-r^2(1-(cosθ)^2)}-rcosθ-(a-r)
={√(49a^2-40r^2)+4r-7a}/7
左端の位置は
f(180°-θ)=√{a^2-r^2(1-(cosθ)^2)}+rcosθ-(a-r)
={√(49a^2-40r^2)+10r-7a}/7
となりますね。
# 計算は御確認下さい。
|